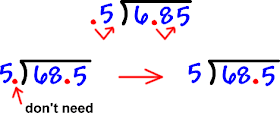MATH
How to add a list of numbers
*Add as usual
*find compliments (numbers that add up to ten)
Example:
9 ١
2 ٢
3 ٢
5 ٢
1 ١
__+
20
Everyone will agree that instead of adding from top to bottom it is faster to look for numbers that add up to ten. 9 & 1 is 10 and so is 5+2 & 3
2 ٣
9 ١
4 ٢
3 ٣
6 ٢
5 ٣
1 ١
_____+
30
Checking off compliments mentally with Eastern Arabic numerals or Hebrew letters may be useful
Pages
▼
Tuesday, September 1, 2015
Thursday, August 27, 2015
ZIG ZAG ADDITION
MATH
YOUTUBE EXPLANATION
429
534
+____
963
*first off, mental addition always goes left to right, starting with the big number. This eliminates the need to juggle borrowing and carrying over.
*next rule is never say the word plus or minus out loud or in your head. Doing so just needlessly clutters your mind. Just repeat values
*simply add from left to right and repeat values
Example:
429
534+
Nine hundred
Nine hundred twenty
Nine hundred fifty
Nine hundred fifty nine
Nine hundred sixty three
Our answer is 963!
-It's that easy! Mental addition is just zig zagging through the problem, repeating the values in a succinct manner until you reach the end.
Let's assume you were adding money. Like 4.29 + 5.34... Simply ignore the decimal points and add normally like in the example. With money all you have to do is put in a decimal point two places from the right when finished so that you have your cents.
*IMPORTANT RULE! When adding money remove the decimal points and treat dollars as hundreds. So instead of saying 4.29 dollars say four hundred twenty nine. This allows you to perform zig zag or mental addition.
YOUTUBE EXPLANATION
429
534
+____
963
*first off, mental addition always goes left to right, starting with the big number. This eliminates the need to juggle borrowing and carrying over.
*next rule is never say the word plus or minus out loud or in your head. Doing so just needlessly clutters your mind. Just repeat values
*simply add from left to right and repeat values
Example:
429
534+
Nine hundred
Nine hundred twenty
Nine hundred fifty
Nine hundred fifty nine
Nine hundred sixty three
Our answer is 963!
-It's that easy! Mental addition is just zig zagging through the problem, repeating the values in a succinct manner until you reach the end.
Let's assume you were adding money. Like 4.29 + 5.34... Simply ignore the decimal points and add normally like in the example. With money all you have to do is put in a decimal point two places from the right when finished so that you have your cents.
*IMPORTANT RULE! When adding money remove the decimal points and treat dollars as hundreds. So instead of saying 4.29 dollars say four hundred twenty nine. This allows you to perform zig zag or mental addition.
Sunday, July 26, 2015
Pi
MATH
before we begin let's get in some relevant Hebrew vocabulary so that we are advancing our Hebraic education in every circumstance
circumference
HeQeF הקף
radius
RaDYuX רדיוס
diameter
Qo9eR קוטר
r: The distance from the center of a circle to any point on the circle is called the radius.
d: The distance across and through the center of a circle is called the diameter.
The diameter is always equal to twice the radius.
If the radius is 3, the diameter is 2 × 3, or 6.
The circumference of a circle is the distance all the way around the outside edge of the circle. In other words, circumference is the name for a circle's perimeter.
A long time ago an Egyptian mind took a rope and cut it equal to the distance through the trunk of a tree. He cut another rope equal to the distance around the trunk of the tree. The rope that equaled the distance around the trunk was three times as long! But wait! Not exactly! It was a little over three times. This magic number is called pi or π. It has the approximate value of 3.14.
FORMULA FOR CIRCUMFERENCE OF A CIRCLE:
πd
FORMULA FOR AREA OF A CIRCLE:
πr^2
before we begin let's get in some relevant Hebrew vocabulary so that we are advancing our Hebraic education in every circumstance
circumference
HeQeF הקף
radius
RaDYuX רדיוס
diameter
Qo9eR קוטר
r: The distance from the center of a circle to any point on the circle is called the radius.
d: The distance across and through the center of a circle is called the diameter.
The diameter is always equal to twice the radius.
If the radius is 3, the diameter is 2 × 3, or 6.
The circumference of a circle is the distance all the way around the outside edge of the circle. In other words, circumference is the name for a circle's perimeter.
A long time ago an Egyptian mind took a rope and cut it equal to the distance through the trunk of a tree. He cut another rope equal to the distance around the trunk of the tree. The rope that equaled the distance around the trunk was three times as long! But wait! Not exactly! It was a little over three times. This magic number is called pi or π. It has the approximate value of 3.14.
FORMULA FOR CIRCUMFERENCE OF A CIRCLE:
πd
FORMULA FOR AREA OF A CIRCLE:
πr^2
Saturday, July 25, 2015
PYTHAGOREAN THEOREM
MATH
before we begin let's get in some relevant Hebrew vocabulary so that we are advancing our Hebraic education in every circumstance
Right angle triangle
M5uLa5 Ya5aR-ZaWiT משולש ישר-זווית
Pythagorean theorem
Mi5Pa9 PiTRaGoX משפט פיתרגוס
Hypotenuse
YeTeR יתר
The three angles inside a triangle always add up to 180°, no matter how the triangle is drawn.
PYTHAGOREAN THEOREM
-A right angle triangle contains one angle that equals 90°.
the sides of a right triangle are always in a particular proportion which can be expressed by the formula A^2 + B^2 = C^2, in which A and B are the two shorter sides of the triangle, and C is the longer side opposite the 90-degree angle. This longer side is called the hypotenuse.
3-4-5 triangle
TESTING THE THEOREM
3^2 + 4^2 should equal 5^2. Does it? Yes! 9 + 16 does equal 25.
before we begin let's get in some relevant Hebrew vocabulary so that we are advancing our Hebraic education in every circumstance
Right angle triangle
M5uLa5 Ya5aR-ZaWiT משולש ישר-זווית
Pythagorean theorem
Mi5Pa9 PiTRaGoX משפט פיתרגוס
Hypotenuse
YeTeR יתר
The three angles inside a triangle always add up to 180°, no matter how the triangle is drawn.
PYTHAGOREAN THEOREM
-A right angle triangle contains one angle that equals 90°.
the sides of a right triangle are always in a particular proportion which can be expressed by the formula A^2 + B^2 = C^2, in which A and B are the two shorter sides of the triangle, and C is the longer side opposite the 90-degree angle. This longer side is called the hypotenuse.
3-4-5 triangle
TESTING THE THEOREM
3^2 + 4^2 should equal 5^2. Does it? Yes! 9 + 16 does equal 25.
GEOMETRY
MATH
before we begin let's get in some relevant Hebrew vocabulary so that we are advancing our Hebraic education in every circumstance
Geometry
Ge4oMe9ReYaH גיאומטריה
perimeter
HeQeF הקף
Area of a rectangle=L × W
Volume of a rectangle=L × W × D
Area of a square=side^2
Volume of a cube=side^3
Perimeter of a rectangle=add all sides
Area of a triangle=base × height ÷ 2
A pyramid is a three-dimensional shape made of four sides that suit atop a rectangular base.
Volume of a pyramid=bh ÷ 3
Finding the volume of a pyramid is just like finding the volume of a rectangle or cube except you divide by three. Why do you divide by three? Because a pyramid is a cube with three as it's strength instead of 4.
before we begin let's get in some relevant Hebrew vocabulary so that we are advancing our Hebraic education in every circumstance
Geometry
Ge4oMe9ReYaH גיאומטריה
perimeter
HeQeF הקף
Area of a rectangle=L × W
Volume of a rectangle=L × W × D
Area of a square=side^2
Volume of a cube=side^3
Perimeter of a rectangle=add all sides
Area of a triangle=base × height ÷ 2
A pyramid is a three-dimensional shape made of four sides that suit atop a rectangular base.
Volume of a pyramid=bh ÷ 3
Finding the volume of a pyramid is just like finding the volume of a rectangle or cube except you divide by three. Why do you divide by three? Because a pyramid is a cube with three as it's strength instead of 4.
Friday, July 24, 2015
Thursday, July 23, 2015
GREATER THAN
before we begin let's get in some relevant Hebrew vocabulary so that we are advancing our Hebraic education in every circumstance
Greater than
GaDoL Me גדול מ
Less than
Qa9aN Me קטן מ
The alligator on the left is greater than any
The tail on the left is less than an inch
Tuesday, July 21, 2015
SQUARE ROOTS
MATH
Square root
5oRe5 MRuBa7 שורש מרובע
RADICALS
The square root of a positive number x is the number that, when squared, equals x.
For example:
The square root of 16 equals 4 because 4 × 4 = 16.
The square root of 9 equals 3 because 3 × 3 = 9.
The square root of 4 equals 2 because 2 × 2 = 4.
The symbol for a positive square root is √, also called a radical.
√16=4
√9=3
Square root
5oRe5 MRuBa7 שורש מרובע
RADICALS
The square root of a positive number x is the number that, when squared, equals x.
For example:
The square root of 16 equals 4 because 4 × 4 = 16.
The square root of 9 equals 3 because 3 × 3 = 9.
The square root of 4 equals 2 because 2 × 2 = 4.
The symbol for a positive square root is √, also called a radical.
√16=4
√9=3
EXPONENT
MATH
Exponent
Ma7aRi2 מעריך
4 Rules of exponents
An exponent is shorthand for multiplication. The large number is called the base, and the little number is called the exponent.
*When you multiply numbers that have the same base, you simply add the exponents.
*When you divide numbers that have the same base, you simply subtract the bottom exponent from the top exponent.
*Anything to the zero power is 1.
*anything to the first power equals that number.
HOW BIG IS A BILLION YOUTUBE
A milliard is 1,000^3 think of a yard having 3 feet
A million is 1,000^2 thus it has six zeros
Exponent
Ma7aRi2 מעריך
4 Rules of exponents
An exponent is shorthand for multiplication. The large number is called the base, and the little number is called the exponent.
*When you multiply numbers that have the same base, you simply add the exponents.
*When you divide numbers that have the same base, you simply subtract the bottom exponent from the top exponent.
*Anything to the zero power is 1.
*anything to the first power equals that number.
HOW BIG IS A BILLION YOUTUBE
A milliard is 1,000^3 think of a yard having 3 feet
A million is 1,000^2 thus it has six zeros
Sunday, July 19, 2015
RATE
MATH
before we begin let's get in some relevant Hebrew vocabulary so that we are advancing our Hebraic education in every circumstance
Rate
5i7uR שיעור
Distance is 50 in the photo
Speed(rate)
50 ÷ .5 = 100
Time
50 ÷ 100 = .5
Distance
100 × .5 = 50
EXAMPLE
A train traveled at a speed of 120 kilometers per hour for 2.5 hours. How many kilometers did the train travel?
R × T = D
120 x 2.5 = 300
In summary: when you are talking about rate it's all about dividing distance
before we begin let's get in some relevant Hebrew vocabulary so that we are advancing our Hebraic education in every circumstance
Rate
5i7uR שיעור
Distance is 50 in the photo
Speed(rate)
50 ÷ .5 = 100
Time
50 ÷ 100 = .5
Distance
100 × .5 = 50
EXAMPLE
A train traveled at a speed of 120 kilometers per hour for 2.5 hours. How many kilometers did the train travel?
R × T = D
120 x 2.5 = 300
In summary: when you are talking about rate it's all about dividing distance
CROSS MULTIPLICATION
MATH
When two fractions have the same exact value, multiplying the numerators by the denominators will give the same answer.
for example:
8/12= 2/3
-these two fractions have the same exact value
8×3=24
12×2=24
This proves they are identical in value
To cross multiply is to go from this:
a/b = c/d
To this:
ad = bc
Knowing this simple fact is useful. With this we can use a technique called 'cross multiplication'. Cross multiplication has two uses
1. It can tell us which of two fractions is larger
2. It can help us solve variables or the missing piece of information in an equation
WHICH IS THE GREATER FRACTION?
Cross-multiplication is a handy math skill to know. You can use it for a few different purposes. For example, you can compare fractions and find out which is greater.
For example, suppose you want to find out which of the following three fractions is the greatest:
3/5 5/9 6/11
Cross-multiplication works only with two fractions at a time, so pick the first two:
3/5 cross multiply with 5/9
3×9=27
5×5=25
Because 27 is greater than 25, you know now that 3/5 is greater than 5/9. So you can throw out 5/9.
Now do the same thing for 3/5 and 6/11:
3/5 cross multiply with 6/11
3×11=33
6×5=30
Because 33 is greater than 30, 3/5 is greater than 6/11. Pretty straightforward, right?
SOLVING VARIABLES
If a 4ft tree cast an 8ft shadow, how long of a shadow does an 8ft tree cast?
4:8 = 8:x
4x = 8×8
4x = 64
x= 16
Remember the formula?
a:b = c:d
Which is:
ad = bc
KNOWN AS THE RULE OF THREE, WAS UNDERSTOOD BY HEBREWS IN THE 15TH CENTURY
When two fractions have the same exact value, multiplying the numerators by the denominators will give the same answer.
for example:
8/12= 2/3
-these two fractions have the same exact value
8×3=24
12×2=24
This proves they are identical in value
To cross multiply is to go from this:
a/b = c/d
To this:
ad = bc
Knowing this simple fact is useful. With this we can use a technique called 'cross multiplication'. Cross multiplication has two uses
1. It can tell us which of two fractions is larger
2. It can help us solve variables or the missing piece of information in an equation
WHICH IS THE GREATER FRACTION?
Cross-multiplication is a handy math skill to know. You can use it for a few different purposes. For example, you can compare fractions and find out which is greater.
For example, suppose you want to find out which of the following three fractions is the greatest:
3/5 5/9 6/11
Cross-multiplication works only with two fractions at a time, so pick the first two:
3/5 cross multiply with 5/9
3×9=27
5×5=25
Because 27 is greater than 25, you know now that 3/5 is greater than 5/9. So you can throw out 5/9.
Now do the same thing for 3/5 and 6/11:
3/5 cross multiply with 6/11
3×11=33
6×5=30
Because 33 is greater than 30, 3/5 is greater than 6/11. Pretty straightforward, right?
SOLVING VARIABLES
If a 4ft tree cast an 8ft shadow, how long of a shadow does an 8ft tree cast?
4:8 = 8:x
4x = 8×8
4x = 64
x= 16
Remember the formula?
a:b = c:d
Which is:
ad = bc
KNOWN AS THE RULE OF THREE, WAS UNDERSTOOD BY HEBREWS IN THE 15TH CENTURY
Weighted mean
MATH
before we begin let's get in some relevant Hebrew vocabulary so that we are advancing our Hebraic education in every circumstance
Weighted Mean
MMu3a7 M5uQLaL ממוצע משוקלל
The weighted mean is used when numbers in a set are not all equally important. Those with more importance are given more weight when calculating the mean, or average. Here's how.
Let's say there are 4 tests in total for a certain class: Exam A, the Midterm Exam, Exam B, and the final Exam. Exam A and B may be worth only 20% each of your final grade, while the Midterm and Final Exams may each be worth 30% of your final grade. You happen to score the following on each:
Exam A-95
Midterm Exam-90
Exam B-92
Final Exam-87
To calculate your final grade for the class, you can't just take the mean (average), since the Midterm and Final exams have more weight than Exams A and B. So you must find the weighted mean. Start by writing the weights next to each corresponding item.
Exam A-95 20%
Midterm Exam-90 30%
Exam B-92 20%
Final Exam-87 30%
Now multiply each score by its weight and write that new value off to the right.
Exam A-95 20% = 1,900
Midterm Exam-90 30% = 2,700
Exam B-92 20& = 1,840
Final Exam-87 30% = 2,610
Add up both the final column and the weights column.
Exam A-95 20% = 1,900
Midterm Exam-90 30% = 2,700
Exam B-92 20& = 1,840
Final Exam-87 30% = 2,610
100% 9,050
Now divide the total value by the total of the weights to get the weighted average.
9050÷100=90.5
Your final grade in class would be 90.5
In summary, you can calculate the weighted mean by following these steps:
STEP 1. Multiply your values by their respective weights
STEP 2. Add all your weights together and all your new values together
STEP 3. Divide the total new value by the total weight.
Not that it's real important but:
For converting percentages into decimals click here
For multiplying decimals click here
before we begin let's get in some relevant Hebrew vocabulary so that we are advancing our Hebraic education in every circumstance
Weighted Mean
MMu3a7 M5uQLaL ממוצע משוקלל
The weighted mean is used when numbers in a set are not all equally important. Those with more importance are given more weight when calculating the mean, or average. Here's how.
Let's say there are 4 tests in total for a certain class: Exam A, the Midterm Exam, Exam B, and the final Exam. Exam A and B may be worth only 20% each of your final grade, while the Midterm and Final Exams may each be worth 30% of your final grade. You happen to score the following on each:
Exam A-95
Midterm Exam-90
Exam B-92
Final Exam-87
To calculate your final grade for the class, you can't just take the mean (average), since the Midterm and Final exams have more weight than Exams A and B. So you must find the weighted mean. Start by writing the weights next to each corresponding item.
Exam A-95 20%
Midterm Exam-90 30%
Exam B-92 20%
Final Exam-87 30%
Now multiply each score by its weight and write that new value off to the right.
Exam A-95 20% = 1,900
Midterm Exam-90 30% = 2,700
Exam B-92 20& = 1,840
Final Exam-87 30% = 2,610
Add up both the final column and the weights column.
Exam A-95 20% = 1,900
Midterm Exam-90 30% = 2,700
Exam B-92 20& = 1,840
Final Exam-87 30% = 2,610
100% 9,050
Now divide the total value by the total of the weights to get the weighted average.
9050÷100=90.5
Your final grade in class would be 90.5
In summary, you can calculate the weighted mean by following these steps:
STEP 1. Multiply your values by their respective weights
STEP 2. Add all your weights together and all your new values together
STEP 3. Divide the total new value by the total weight.
Not that it's real important but:
For converting percentages into decimals click here
For multiplying decimals click here
Friday, July 17, 2015
MODE
MATH
before we begin let's get in some relevant Hebrew vocabulary so that we are advancing our Hebraic education in every circumstance
mode
5a2iaC שכיח
The mode of a set of numbers is the number that appears the most often.
If there were 24 traffic summonses issued in September, 45 in October, 24 in November, and 39 in December, what was the mode number of summonses issued over the three months?
Here's how to Crack It
First, put the numbers in ascending order: 24, 24, 39, 45
The correct answer is 24
before we begin let's get in some relevant Hebrew vocabulary so that we are advancing our Hebraic education in every circumstance
mode
5a2iaC שכיח
The mode of a set of numbers is the number that appears the most often.
If there were 24 traffic summonses issued in September, 45 in October, 24 in November, and 39 in December, what was the mode number of summonses issued over the three months?
Here's how to Crack It
First, put the numbers in ascending order: 24, 24, 39, 45
The correct answer is 24
PERCENTS
MATH
before we begin let's get in some relevant Hebrew vocabulary so that we are advancing our Hebraic education in every circumstance
Percent
4aCuZ אחוז
FINDING PERCENTS OF A NUMBER
To find 10% of any number, all you have to do is move the decimal point of that number over one place to the left.
What is 10% of 30?
10% of 30 = 3
So how much is 20% of 30? That's easy. It's twice as much as 10 percent, or 6.
What is 20% of 520?
10% of 520 = 52, so 20% of 520 = 104
To find 1 percent of any number, all you have to do is move the decimal point of that number over two places to the left.
1% of 4 = 0.04
1% of 520 = 5.2
In just the same way we found 20 percent by doubling 10 percent, we can now find 2 percent by doubling 1 percent.
What is 2% of 500?
1% of 500 = 5, so 2% of 500 = 2 × 5 = 10
Now, here's the really great part. We can combine these two techniques to find any percentage test writers can invent.
Let's find 23% of 600
Well, 10% of 600 = 60
So 20% of 600 = 2 × 60 = 120
And 1% of 600 = 6, so 3% of 600 = 18
So what is 23% of 600?
20% of 600 = 120
3% of 600 =18
120 + 18 = 138
CONVERTING PERCENTS TO DECIMALS
Note: A percentage is just a fraction whose denominator is always 100.
Percent
4aCuZ אחוז
FINDING PERCENTS OF A NUMBER
To find 10% of any number, all you have to do is move the decimal point of that number over one place to the left.
What is 10% of 30?
10% of 30 = 3
So how much is 20% of 30? That's easy. It's twice as much as 10 percent, or 6.
What is 20% of 520?
10% of 520 = 52, so 20% of 520 = 104
To find 1 percent of any number, all you have to do is move the decimal point of that number over two places to the left.
1% of 4 = 0.04
1% of 520 = 5.2
In just the same way we found 20 percent by doubling 10 percent, we can now find 2 percent by doubling 1 percent.
What is 2% of 500?
1% of 500 = 5, so 2% of 500 = 2 × 5 = 10
Now, here's the really great part. We can combine these two techniques to find any percentage test writers can invent.
Let's find 23% of 600
Well, 10% of 600 = 60
So 20% of 600 = 2 × 60 = 120
And 1% of 600 = 6, so 3% of 600 = 18
So what is 23% of 600?
20% of 600 = 120
3% of 600 =18
120 + 18 = 138
CONVERTING PERCENTS TO DECIMALS
the short way to convert from a percentage to a decimal is by removing the percentage sign and moving the decimal point 2 places to the left.
Note: A percentage is just a fraction whose denominator is always 100.
Thursday, July 16, 2015
ADDING OR SUBTRACTING FRACTIONS BUTTERFLY TECHNIQUE
MATH
+/- fractions butterfly technique
טריק פרפר
Step 1. Draw wings
Step 2. Draw body over operation sign
Step 3. Draw plus or minus (depending on addition or subtraction) sign for antenna
Step 4. Draw multiplication sign for tail
Step 5. Multiply the wings
APPLY THE OPERATIONS IN THE HEAD AND THE TAIL
Step 6. Use head to add (or subtract) wings
Step 7. Multiply the tail
+/- fractions butterfly technique
טריק פרפר
Step 1. Draw wings
Step 2. Draw body over operation sign
Step 3. Draw plus or minus (depending on addition or subtraction) sign for antenna
Step 4. Draw multiplication sign for tail
Step 5. Multiply the wings
APPLY THE OPERATIONS IN THE HEAD AND THE TAIL
Step 6. Use head to add (or subtract) wings
Step 7. Multiply the tail
MULTIPLYING AND DIVIDING DECIMALS
MATH
before we begin let's get in some relevant Hebrew vocabulary so that we are advancing our Hebraic education in every circumstance
Quotient
MaNaH מנה
Divisor
MCaLeQ מחלק
Dividend
MCuLaQ מחולק
To multiply decimals
Just follow these steps:
Step 1 Multiply normally, ignoring the decimal points.
Step 2 Then put the decimal point in the answer - it will have as many decimal places as the two original numbers combined.
before we begin let's get in some relevant Hebrew vocabulary so that we are advancing our Hebraic education in every circumstance
Quotient
MaNaH מנה
Divisor
MCaLeQ מחלק
Dividend
MCuLaQ מחולק
To multiply decimals
Just follow these steps:
Step 1 Multiply normally, ignoring the decimal points.
Step 2 Then put the decimal point in the answer - it will have as many decimal places as the two original numbers combined.
To divide decimal numbers:
Step 1: If the divisor is not a whole number, move decimal point to right to make it a whole number and move decimal point in dividend the same number of places.
Step 2: Divide as usual. ...
Step 3: Put decimal point directly above decimal point in the dividend.
Step 4: Check your answer.
So 6.85 ÷ .5 = 13.7
FRACTION TO DECIMAL DECIMAL TO FRACTION
MATH
To turn a fraction into a decimal simply divide the top by the bottom
You can also convert any decimal into a fraction. The first digit to the right of the decimal is the tenths'place. The second decimal is the hundredths place. Consider this example:
To turn a fraction into a decimal simply divide the top by the bottom
You can also convert any decimal into a fraction. The first digit to the right of the decimal is the tenths'place. The second decimal is the hundredths place. Consider this example:
Wednesday, July 15, 2015
CONVERT MIXED FRACTION
MATH
To convert a mixed fraction to an improper fraction, follow these steps:
Step 1 Multiply the whole number part by the fraction's denominator.
Step 2 Add that to the numerator.
Step 3 Write that result on top of the denominator.
To convert a mixed fraction to an improper fraction, follow these steps:
Step 1 Multiply the whole number part by the fraction's denominator.
Step 2 Add that to the numerator.
Step 3 Write that result on top of the denominator.
Multiplying and dividing fractions
MATH
To multiply fractions, line them up and multiply straight across
5/6 × 4/5 = 20/30 = 2/3
Cancel method
We can save work when multiplying fractions if we cancel first. Canceling is a way to simplify fractions before we multiply. Find one numerator and one denominator that are divisible by the same number. You must always cancel diagonally, never horizontally.
Dividing fractions
To divide one fraction by another, just invert the second fraction and multiply.
2/3 ÷ 3/4 is the same as 2/3 × 4/3 = 8/9
To multiply fractions, line them up and multiply straight across
5/6 × 4/5 = 20/30 = 2/3
Cancel method
We can save work when multiplying fractions if we cancel first. Canceling is a way to simplify fractions before we multiply. Find one numerator and one denominator that are divisible by the same number. You must always cancel diagonally, never horizontally.

Dividing fractions
To divide one fraction by another, just invert the second fraction and multiply.
2/3 ÷ 3/4 is the same as 2/3 × 4/3 = 8/9
LEAST COMMON DENOMINATOR BOWTIE TECHNIQUE
MATH
When adding fractions, if the common denominator is simply the result of multiplying both denominators together, than you can use the 'bowtie technique' for the numerators or MoNoT.
When adding fractions, if the common denominator is simply the result of multiplying both denominators together, than you can use the 'bowtie technique' for the numerators or MoNoT.
LEAST COMMON DENOMINATOR
MATH
before we begin let's get in some relevant Hebrew vocabulary so that we are advancing our Hebraic education in every circumstance
Numerator
MoNeH מונה
Denominator
M2aNeH מכנה
The denominator is the bottom number in a fraction.
It shows how many equal parts the item is divided into
You can't add fractions with different denominators:
So what do you do? How can they be added?
Answer: You need to make the denominators the same.
Here are the steps to follow:
STEP 1. Find the Least Common Multiple of the denominators (which is called the Least Common Denominator).
STEP 2. Change each fraction (using equivalent fractions) to make their denominators the same as the least common denominator. (Involves multiplying the top and bottom numbers).
STEP 3. Then add (or subtract) the fractions, as you wish!
Example: What is 1/6 + 7/15 ?
The Denominators are 6 and 15:
multiples of 6: 6, 12, 18, 24, 30, 36, ...
multiples 15: 15, 30, 45, 60, ...
***So the Least Common Multiple of 6 and 15 is 30.
Now let's try to make the denominators the same.
Note: what you do to the bottom of the fraction,
you must also do to the top
***When you multiply 6 × 5 you get 30, and when you multiply 15 × 2 you also get 30:
***Now we can do the addition by adding the top numbers:
5/30 + 14/30 = 19/30
The fraction is already as simple as it can be, so that is the answer.
before we begin let's get in some relevant Hebrew vocabulary so that we are advancing our Hebraic education in every circumstance
Numerator
MoNeH מונה
Denominator
M2aNeH מכנה
The denominator is the bottom number in a fraction.
It shows how many equal parts the item is divided into
You can't add fractions with different denominators:
So what do you do? How can they be added?
Answer: You need to make the denominators the same.
Here are the steps to follow:
STEP 1. Find the Least Common Multiple of the denominators (which is called the Least Common Denominator).
STEP 2. Change each fraction (using equivalent fractions) to make their denominators the same as the least common denominator. (Involves multiplying the top and bottom numbers).
STEP 3. Then add (or subtract) the fractions, as you wish!
Example: What is 1/6 + 7/15 ?
The Denominators are 6 and 15:
multiples of 6: 6, 12, 18, 24, 30, 36, ...
multiples 15: 15, 30, 45, 60, ...
***So the Least Common Multiple of 6 and 15 is 30.
Now let's try to make the denominators the same.
Note: what you do to the bottom of the fraction,
you must also do to the top
***When you multiply 6 × 5 you get 30, and when you multiply 15 × 2 you also get 30:
***Now we can do the addition by adding the top numbers:
5/30 + 14/30 = 19/30
The fraction is already as simple as it can be, so that is the answer.
Tuesday, July 14, 2015
DISTRIBUTIVE PROPERTY
MATH
COMBINING LIKE TERMS YOUTUBE
The distributive property states that
a(b + c) = ab + ac and a(b - c) = ab - ac
Example: 3(4 + 2) = 3(4) + 3(2) = 18
Example: 3(4 - 2) = 3(4) - 3(2) = 6
If 3X + 3Y = 21, then what is the value of X + Y?
A. 3
B. 6
C. 7
D. Not enough information is given
3X + 3Y= 3(X + Y) = 21
Three times what number equals 21? The answer is 7.
COMBINING LIKE TERMS YOUTUBE
The distributive property states that
a(b + c) = ab + ac and a(b - c) = ab - ac
Example: 3(4 + 2) = 3(4) + 3(2) = 18
Example: 3(4 - 2) = 3(4) - 3(2) = 6
If 3X + 3Y = 21, then what is the value of X + Y?
A. 3
B. 6
C. 7
D. Not enough information is given
3X + 3Y= 3(X + Y) = 21
Three times what number equals 21? The answer is 7.
MULTIPLY AND DIVIDE POSITIVE AND NEGATIVE NUMBERS HEBREWIZED
before we begin let's get in some relevant Hebrew vocabulary so that we are advancing our Hebraic education in every circumstance
Positive
CiYuVi חיובי
Positive
CiYuVi חיובי
Negative
5LiLi שלילי
MNEMONIC: Think Deu 22:11 mix= bad
5LiLi שלילי
MNEMONIC: Think Deu 22:11 mix= bad
MULTIPLICATION כפל KeFeL
positive × positive = positive 2 × 3 = 6
positive × positive = positive 2 × 3 = 6
positive × negative = negative 2 × -3 = -6
negative × positive = negative -2 × 3 = -6
negative × negative = positive -2 × -3 = 6
DIVISION חילוק CiLuQ
positive ÷ positive = positive 6 ÷ 2 = 3
positive ÷ positive = positive 6 ÷ 2 = 3
positive ÷ negative = negative 6 ÷ -2 = -3
negative ÷ positive = negative -6 ÷ 2 = -3
negative ÷ negative = positive -6 ÷ -2 = 3
DIVIDING FRACTIONS HEBREWIZED
MATH
before we begin let's get in some relevant Hebrew vocabulary so that we are advancing our Hebraic education in every circumstance
Fraction
5eVeR Pa5u9 שבר פשוט
Formula
NuXCaH נוסחה
Formula:
Leave me/change me/turn me over
1/2 ÷ 1/6
Becomes
1/2 × 6/1= 6/2=3
FURTHER DETAIL
Step 1. Turn the second fraction upside down (the reciprocal):
1/6 becomes 6/1
Step 2. Multiply the first fraction by that reciprocal:
1/2 × 6/1=1×6/2×1=6/2
Step 3. Simplify the fraction:
6/2=3
Fractions and Whole Numbers
What about division with fractions and whole numbers?
Make the whole number a fraction, by putting it over 1.
Example: 5 is also 5/1
Then continue as before.
Example:
2/3÷5
Make 5 into 5/1 :
2/3÷5/1
Step 1. Turn the second fraction upside down (the reciprocal):
5/1 becomes 1/5
Step 2. Multiply the first fraction by that reciprocal:
2/3×1/5=2 × 1/3 × 5=2/15
Step 3. Simplify the fraction:
The fraction is already as simple as it can be.
Answer = 2/15
Why Turn the Fraction Upside Down?
Because dividing is the opposite of multiplying!
So instead of dividing by a fraction, it is easier to turn that fraction upside down, then do a multiply.
before we begin let's get in some relevant Hebrew vocabulary so that we are advancing our Hebraic education in every circumstance
Fraction
5eVeR Pa5u9 שבר פשוט
Formula
NuXCaH נוסחה
Formula:
Leave me/change me/turn me over
1/2 ÷ 1/6
Becomes
1/2 × 6/1= 6/2=3
FURTHER DETAIL
Step 1. Turn the second fraction upside down (the reciprocal):
1/6 becomes 6/1
Step 2. Multiply the first fraction by that reciprocal:
1/2 × 6/1=1×6/2×1=6/2
Step 3. Simplify the fraction:
6/2=3
Fractions and Whole Numbers
What about division with fractions and whole numbers?
Make the whole number a fraction, by putting it over 1.
Example: 5 is also 5/1
Then continue as before.
Example:
2/3÷5
Make 5 into 5/1 :
2/3÷5/1
Step 1. Turn the second fraction upside down (the reciprocal):
5/1 becomes 1/5
Step 2. Multiply the first fraction by that reciprocal:
2/3×1/5=2 × 1/3 × 5=2/15
Step 3. Simplify the fraction:
The fraction is already as simple as it can be.
Answer = 2/15
Why Turn the Fraction Upside Down?
Because dividing is the opposite of multiplying!
So instead of dividing by a fraction, it is easier to turn that fraction upside down, then do a multiply.
Monday, July 13, 2015
My dictionary
MATH
ALGEBRA
4aLGEBRA אלגברה
GiBuR גיבור
HERO
variable: x and y
Mi5TaNeH משתנה
Coefficients: number part of algebra equation
MQaDeM מקדם
-from QiDeM קדם to advance. Since the coefficient comes before the variable.
Constant: number in an algebraic expression without variables
QaVua7 קבוע
-From QeVa7 קבע permanent
Integer: a whole number that's positive or negative
MiXPaR 5aLeM מספר שלם
ALGEBRA
4aLGEBRA אלגברה
GiBuR גיבור
HERO
variable: x and y
Mi5TaNeH משתנה
Coefficients: number part of algebra equation
MQaDeM מקדם
-from QiDeM קדם to advance. Since the coefficient comes before the variable.
Constant: number in an algebraic expression without variables
QaVua7 קבוע
-From QeVa7 קבע permanent
Integer: a whole number that's positive or negative
MiXPaR 5aLeM מספר שלם
ABACUS
MATH
before we begin let's get in some relevant Hebrew vocabulary so that we are advancing our Hebraic education in every circumstance
Abacus
Ce5boniyah חשבוניה
Little friend and family are based off 5
Big friend is based off 10
Little friend is 1-4
Family is 6-9
Big friend is 1-9
*rule if you can do little friend, big friend or family than it is correct
before we begin let's get in some relevant Hebrew vocabulary so that we are advancing our Hebraic education in every circumstance
Abacus
Ce5boniyah חשבוניה
Little friend and family are based off 5
Big friend is based off 10
Little friend is 1-4
Family is 6-9
Big friend is 1-9
*rule if you can do little friend, big friend or family than it is correct
MATH
- RANDOM(HACKPAD)
- FRACTIONS(HACKPAD)
- Average(blog)
- WEIGHTED MEAN(blog)
- MODE(blog)
- DECIMALS TO FRACTIONS: math is fun
- FRACTION TO DECIMAL DECIMAL TO FRACTION(blog)
- MULTIPLY AND DIVIDE POSITIVE AND NEGATIVE NUMBERS HEBREWIZED(blog)
- DISTRIBUTIVE PROPERTY(blog)see FACTORING POLYNOMIALS
- MULTIPLYING AND DIVIDING DECIMALS(blog)
- PERCENTS(blog)
- CROSS MULTIPLICATION(blog)
- RATE(blog)
- PERCENTAGE RATE & BASE(blog)
- EXPONENT(blog)
- SQUARE ROOTS(blog)
- SCIENTIFIC NOTATION: math is fun
- GREATER THAN(blog)
- PEMDAS(blog)
- FOIL(blog)
- FACTORING POLYNOMIALS see DISTRIBUTIVE PROPERTY
- GEOMETRY(blog)
- PYTHAGOREAN THEOREM(blog)
- Pi(blog)
- ZIGZAG ADDITION (MENTAL MATH BLOG)
- ADDING A LIST (MENTAL MATH BLOG) h
Friday, July 10, 2015
Find Average
MATH
before we begin let's get in some relevant Hebrew vocabulary so that we are advancing our Hebraic education in every circumstance
Average
MMu3a7 ממוצע
To find the average (also know as the mean) simply add them up and divide by how many there are.
before we begin let's get in some relevant Hebrew vocabulary so that we are advancing our Hebraic education in every circumstance
Average
MMu3a7 ממוצע
To find the average (also know as the mean) simply add them up and divide by how many there are.
Cash register
MATH
before we begin let's get in some relevant Hebrew vocabulary so that we are advancing our Hebraic education in every circumstance
Cash register
QuPaH קופה
If you can solve this problem you can work a cash register.
before we begin let's get in some relevant Hebrew vocabulary so that we are advancing our Hebraic education in every circumstance
Cash register
QuPaH קופה
If you can solve this problem you can work a cash register.
Customer buys something for $6.35 and he gives you $20.25
How do you give him the correct change?
Don't do it conventionally
$20.25-6.35
On a register it is the opposite. Start with 6.35-25=$6.10+(90)=$7+(3)=10+(10)=20
Answer $13.90
$20.25-6.35
On a register it is the opposite. Start with 6.35-25=$6.10+(90)=$7+(3)=10+(10)=20
Answer $13.90
EXPLANATION 2
A cashier is able to gather the change in their hands as they calculate because they start with 6.35. Just subtract the 25¢cents from 35 now you got $6.10.... Now the equation begins. Pull 90¢ from drawer and you are at 7$, pull $3 from drawer and you are at $10, lastly pull $10 from drawer and you are at $20(we subtracted ¢25 earlier).... Giving the total of 13.90 without having to stop and use paper or a calculator.